Suffix Trees

Rahul Pandey | February 14, 2017

The suffix tree, invented in 1973, is probably the most powerful and versatile data structure for string processing. The suffix tree represents all the suffixes of a string S in O(n) space and can be built in O(n) time, where n is the length of the string.

Summary
Suffix Tries
Suffix Trees v1
Suffix Trees v2
Building
Generalized Suffix Trees
Real World Application

Summary

A suffix tree is a compressed trie containing all the suffixes of a given text as keys, and positions in the text as their values. We’ll unpack what that means, but suffix trees enable particularly fast implementations of many important string operations, such as:

Find a substring in string S, even if we want to allow a certain number of mistakes in the substring.
Locating matches for a regular expression pattern within a string.
A linear time solution for the longest common substring problem.

The tradeoff for this power is that the storage for a string’s suffix tree requires several multiples more space than storing the string itself.

Suffix Tries

Let’s start by talking about a suffix trie, which isn’t a very practical data structure but it helps us better understand the tree in the next section. The suffix trie is the smallest tree such that:

each edge is labeled with a character c in the alphabet Σ
each node has at most 1 outgoing edge labeled with c, for any c in Σ
each suffix of the tree is “spelled out” along some path starting at the root of the tree

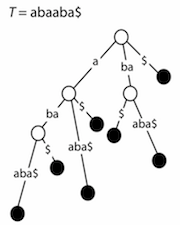
Here is the suffix trie for the string abaaba. The symbol $ indicates the end of the word.

Suffix trie

Take, for example, the suffix ba. If we trace its path in the tree, we find two branches at that node, one with a $ (indicating that this is a suffix), and another branch which indicates that ba is a substring elsewhere in the string.

Try answering these questions about the suffix trie:

How do we count the number of times a string S occurs as a substring of T?

Follow the path corresponding to S (answer is 0 if we fall off the tree) to the node n, and the answer is the # of leaf nodes in the subtree rooted at n. Try this out with the aba and you should see the answer is 2.

How do we find the longest repeated substring of T?

The depth of the tree represents the length of the substring, so we want to find the node of highest depth in T which has more than 1 child (indicating that it is repeated). In this case, the answer is aba, since it is the only substring corresponding to a node of depth 3 with 2 children.

The downside of a suffix trie is that the amount of space required to store the trie grows quadratically with respect to the length of the input string. So for even relatively small strings, say 500 characters, the number of nodes required in the trie could be more than 100K. This leads us to a suffix tree, which compresses the tree.

Suffix Trees v1

The suffix tree is very similar to the trie, except we coalesce non-branching paths into a single edge with a string label (so we have strings on edges instead of characters). This reduces the number of nodes and edges in the tree, and guarantees that internal nodes have > 1 child.

So now our string abaaba has this suffix tree:

Suffix tree1

Some observations about the number of nodes in the trie:

Leaf nodes: There should be exactly n + 1 leaves in the tree since there are n + 1 possible substrings (the empty string, plus the substring starting at each character).
Internal nodes: Since each internal (non-leaf) node has at least 2 children, we know the upper bound on the number of internal nodes will be the number of internal nodes in a full binary tree (i.e. the suffix tree will certainly not be as compact as the binary tree). Think about a full binary tree of height 2 having 2 leaf nodes (1 internal), height 3 having 4 leaf nodes (3 internal), and height 4 having 8 leaf nodes (7 internal). In a binary tree of height h, the number of leaf nodes is 2^h and internal nodes is 2^h - 1. For us, since we know the number of leaf nodes is n + 1, this means we have ≤ n internal nodes.
Summing the above, we have an upper bound on the number of nodes in the suffix tree to be ≤ 2n + 1 = O(n).

However, if you add the lengths of all the strings on the edges, the storage space is still O(n²) edges, so we don’t have a linear space construction yet.

Suffix Trees v2

Instead of having strings labelling the edges, we simply store a pair of numbers: the start and end index for where the substring first occurs in the string. The leaves will store the offset of the suffix that the leaf corresponds to– each leaf will thus have a label from 1 to n of which suffix in the tree it represents. So the final suffix tree looks like this:

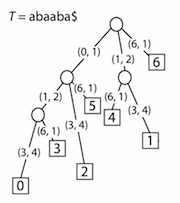
Suffix tree2

Formally, the suffix tree for a string S of length n is defined as a tree such that:

The tree has exactly n leaves numbered from 1 to n.
Except for the root, every internal node has at least two children.
Each edge is labeled with a non-empty substring of S.
No two edges starting out of a node can have string-labels beginning with the same character.
The string obtained by concatenating all the string-labels found on the path from the root to leaf i spells out suffix S[i..n], for i from 1 to n.

Building

We don’t want to build the suffix tree how we described it, since building a suffix trie would need at least O(n²) time and space for each of the O(n²) nodes.

We can improve on this by building up the suffix tree by walking forward through the string. We build a single-edge tree representing only the longest suffix, then augment to include the 2nd longest, then augment to include the 3rd longest, and so on. While this is linear in terms of space usage, this approach is still O(n²) time.

There is a remarkable algorithm called Ukkonen’s algorithm which can construct the suffix tree in O(n) time and space! We won’t discuss it here (it has lots of casework), but check out the reference if you want to learn more about it. Furthermore, Ukkonen’s algorithm provides an “online” construction, which means it will construct the suffix tree as you provide it the characters of your string one character at a time.

Generalized Suffix Trees

Generalized suffix trees are when we build a suffix tree over multiple strings composed together. This is how we actually solve the longest common substring problem in linear time. If we want to find the longest common substring of two string X and Y, we generate the suffix tree for X#Y$, where # and $ are the two special end of string characters. Once we have built up the suffix tree (using Ukkonen’s Algorithm), we need to find the deepest node which has leaves corresponding to indices in both string X and Y (which we’d know from the lengths of the strings). This operation requires a depth-first search, which is still linear in time and space.

You can see the power and versatility that emerge from this construction!

Real World Application

Suffix trees are ideal anytime we can afford to spend a lot of time pre-processing the text, but we want to answer queries about the text very quickly.

One important use for suffix trees is in bioinformatics, where we often want to search for patterns in DNA or protein sequences (which can be viewed as strings of characters). In these applications, we generally want to find a short string (called the pattern) among a much larger string (simply called the string), either with exact or inexact matching.

Another use of suffix trees is to find the longest common substring among a set of strings, or even longest common subsequence (that requires a bit more finagling). They are also commonly used to identify repetitive structures, as is often the case in human genomes. In fact, suffix trees are used in some data compression algorithms because of their ability to identify repeated data.